1
1
L’Analyse en Composantes Principales (ACP) établit automatiquement une typologie de votre territoire, clients, prospects, magasins, etc. à partir de multiples critères chiffrés (Age, chiffre d’affaire, taille d’entreprise, etc.), de manière à déterminer ceux qui présentent des similitudes. Elle permet aussi de mettre en évidence les critères les plus déterminantes dans ces ressemblances.
L’Analyse en Composantes Principales (ACP) en détail
L’Analyse en Composantes Principales (ACP) permet d’étudier simultanément plusieurs données continues (les variables) connues sur des territoires (les individus), avec pour objectif d’identifier :
- les variables fortement corrélées/anti-correlées entre elles. Les individus semblables/dissemblables vis à vis de l’ensemble de ces variables. Les variables les plus/moins explicatives de ces ressemblances entre les individus étudiés.
- connaître les variables les plus explicatives et les plus corrélées permet d’éliminer celles qui sont inutiles ou redondantes, et de résumer et hiérarchiser l’ensemble des informations de la matrice (le tableau de variables et des individus) en vue d’établir une typologie des individus.
L’ACP permet, par exemple, d’étudier les ressemblances entre des quartiers d’une ville par rapport à des données de population, de catégories socioprofessionnelles, de revenus, de logement, d’age, de composition des ménages, etc… Dans ce cas d’étude, les variables de revenus, de CSP et de logement ont une forte probabilité d’être corrélées entre elles. L’analyse des résultats de l’ACP révélera ces corrélations et leur force, permettant ainsi de ne conserver que les variables réellement explicatives et résumant les axes principaux de ressemblance entre les quartiers.
Méthode de calcul de l’ACP avec Cartes & Données
L’ACP effectue les calculs suivants (avec « n » = nombre d’individus, et « p »= nombre de variables) :
- standardisation des données, à savoir les données sont centrées et réduites (xi = (xi – moyenne de x)/écart-type de x).
- constitution de la matrice de corrélation entre les variables. Cette matrice est carrée symétrique d’ordre p (dans la case (i,j), on place le coefficient de corrélation entre la variable i et la variable j).
- détermination des vecteurs propres de la matrice de corrélation, ainsi que leur valeur propre associée.
- calcul des coordonnées des individus et des variables sur ces vecteurs, pour la représentation graphique.
- calcul des autres paramètres (voir ci-dessous).
Interprétation
Les vecteurs propres calculés pour la matrice donnent les axes factoriels. Chaque axe « concentre » un peu de chacune des variables avec plus ou moins d’importance, et résume ainsi plus ou moins bien les informations de la matrice.
Analyser les résultats de l’ACP consiste donc à :
- déterminer le nombre d’axes réellement utiles à l’analyse
- caractériser chacun des axes retenus selon les informations qu’il résume
- étudier comment se positionnent les variables et les individus vis à vis des axes retenu
Déterminer le nombre d’axes
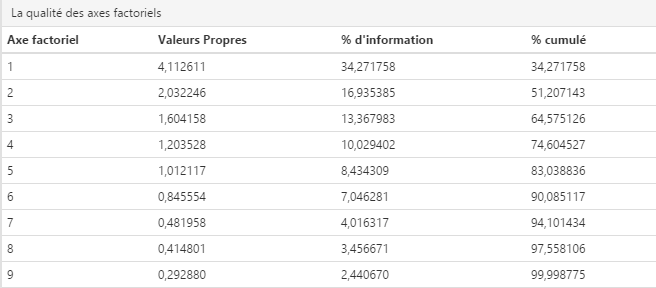
La valeur propre d’un axe permet de déterminer le pourcentage d’information de la matrice qu’il résume. Dans l’ACP, les axes sont numérotés selon un pourcentage d’information décroissant. Nb : l’axe n°1 est toujours celui qui résume le plus d’informations de la matrice.
Il vous faut retenir assez d’axes pour expliquer suffisant d’informations de la matrice. Le pourcentage cumulé des informations résumées par chaque axe fournit une indication dans ce but : vous devez en effet retenir un nombre d’axes suffisant pour résumer au moins 75% des informations de la matrice. A titre d’exemple dans le tableau ci-dessus, on conservera seulement les 5 premiers axes (76,9%), puisqu’ils sont suffisants pour résumer en cumulé plus de 75% des informations.
Vous pourrez en prime choisir 2 des axes retenus (généralement les 2 premiers) pour permettre la représentation graphique des variables et des individus. Les axes factoriels servent alors d’abscisses et d’ordonnées pour positionner les variables ou les individus les uns par rapport aux autres.
Caractériser les axes
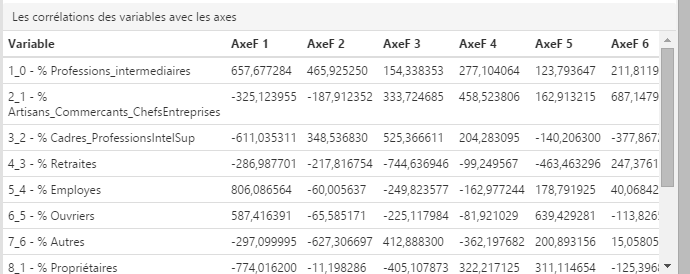
Chaque axe se compose plus ou moins fortement de chacune des variables. Une fois que vous connaissez le nombre d’axes nécessaires pour expliquer suffisamment de ressemblances et d’informations de la matrice, vous devez déterminer pour chaque axe quelles sont les variables qui les définissent le mieux. Le tableau de corrélation des variables avec les axes indique pour chaque variable une valeur positive ou négative sur chaque axe. Plus une variable possède une valeur fortement positive ou négative, plus elle caractérise un axe. Plus une variable possède une valeur proche de « 0 », moins elle caractérise un axe.
Dans l’exemple ci-dessus, l’axe 1 est fortement caractérisé :
- d’un côté, par les variables « Professions intermédiaires », « Employés », « Ouvriers » et « Locataires »
- de l’autre, par les variables « Cadres & professions intellectuelles supérieures » et « Propriétaires »
Etudier le positionnement des individus et des variables
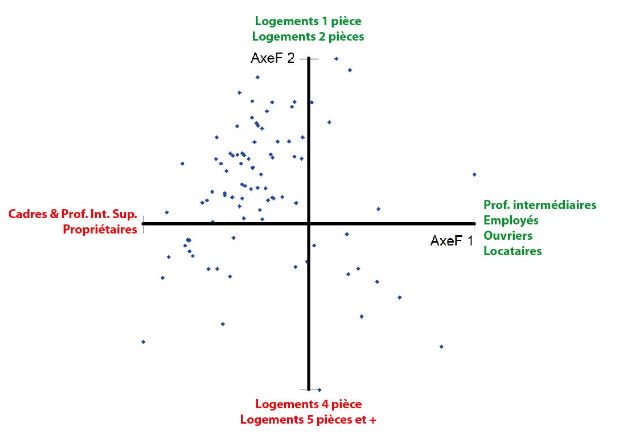
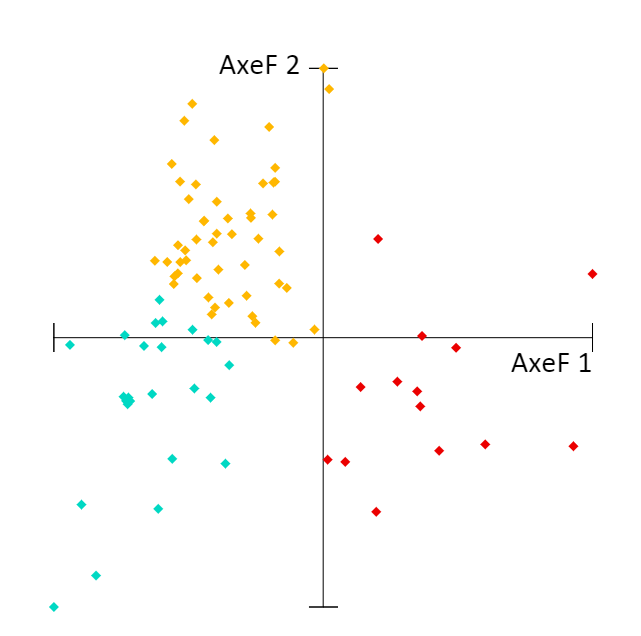
En procédant de la même manière pour caractériser les axes suivants, ceux-ci vous permettent de construire des graphiques qui aident à l’étude de la répartition des individus (points bleus) vis-à-vis de l’ensemble des variables étudiées.
Dans cet exemple, vous constaterez que la majorité des quartiers étudiés (les individus, en points bleus) sont plutôt marqués par des proportions importantes de logements 1 à 2 pièces, de propriétaires, et de cadres/professions intellectuelles supérieures.
L’utilisation de différents axes permet de construire plusieurs versions du même graphique, afin d’observer la répartition des individus ou des variables selon différents « points de vue ». Ainsi, l’ACP permet de comprendre quelles sont les variables les plus significatives pour les territoires étudiés, et comment ces territoires se répartissent vis-à-vis de ces variables.
Résultats
L’ACP est généralement utilisée en préambule d’une méthode de classification des individus pour que cette dernière travaille sur des données résumées et « pré-travaillées ». Par défaut, les résultats du module ne se représentent donc pas sur la carte, puisque celui-ci ne produit pas à proprement parler de donnée « localisée ».
Vous pouvez relier le module ACP à un module CAH pour effectuer la classification des individus en exploitant dans la CAH les résultats de l’ACP (le pré-traitement et le résumé des données).
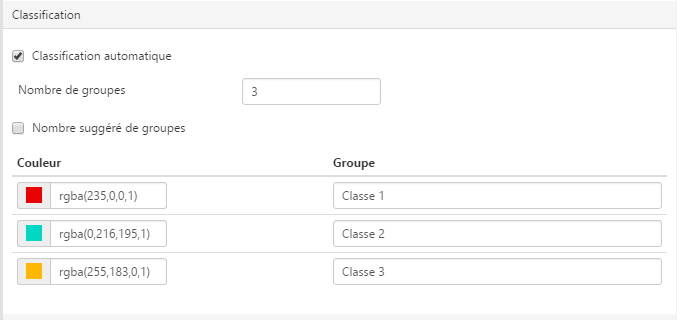
Vous pouvez également effectuer la classification directement dans le module ACP, à l’aide de la méthode K-means : l’algorithme K-means de partitionnement de données est une méthode dont le but est de diviser des observations en K partitions (clusters) dans lesquelles chaque observation appartient à la partition avec la moyenne la plus proche.
Articque est le pionnier français de la prise de décision stratégique grâce à la cartographie. Editeur de solutions géodécisionnelles depuis plus de 30 ans, nous aidons les organismes et entreprises à mieux piloter leurs activités et à éclairer leurs décisions. Elles gagnent ainsi en performance grâce à une connaissance approfondie de leur territoire.
ARTICQUE - TOURS,
149 avenue du Général de Gaulle,
37230 Fondettes – France
02 47 49 90 49