Qu’est-ce que le module Discrétisation ?
Le module Discrétisation permet de diviser manuellement ou automatiquement une donnée chiffrée selon des classes (fourchettes de valeurs) adaptées. Cette opération est idéale pour simplifier la lecture d’une donnée statistique sur la carte, notamment lorsque l’on souhaite la représenter avec un dégradé de couleurs.
Le module vous propose différentes méthodes automatiques pour diviser vos données selon des classes qui représentent au mieux leur dispersion. Vous pouvez également paramétrer manuellement des bornes de classes adaptées à vos problématiques.
Que vous soyez statisticien chevronné ou novice, un indicateur visuel et de nombreux indices statistiques vous guident pour choisir à coup sûr des découpages pertinents de vos données.
Description du module Discrétisation
La discrétisation ou « découpage en classes » vise à simplifier des données brutes (données continues) en rassemblant les valeurs qui sont proches ou se ressemblent en différentes classes, présentées sous forme de fourchettes de valeurs (ex : [de 0 à 10], [de 10 à 25], [de 25 à 33], etc.).
Le résultat d’une discrétisation est une série de données discrètes, c’est-à-dire des données discontinues mises en classes.
La discrétisation est une opération subjective, qui peut aboutir à des résultats différents en fonction des choix de découpage des classes effectués (elle doit donc être utilisée avec précaution) :
- Il n’y a pas à proprement parler de « bonne » ou de « mauvaise » discrétisation.
- Pour être efficace, une discrétisation doit s’efforcer d’être la moins subjective possible, pour être intéressante et retranscrire la réalité des données.
- Une discrétisation « objective » consisterait donc à créer les classes qui rassemblent de manière homogène les valeurs qui se ressemblent, tout veillant à ce que ces classes soient les plus distinctes possible.
L’utilisation d’une discrétisation constitue, en outre, le seul moyen de représenter en dégradé de couleurs des données initialement continues à l’aide d’un module Remplissage.
Cartes & Données propose 7 méthodes de discrétisation
Méthode Standard
La discrétisation est faite selon la loi de Gauss sur les valeurs de la donnée. Les classes sont centrées sur la moyenne arithmétique. Elles sont de largeur un écart-type par défaut, mais vous pouvez choisir comme largeur 2 fois, 3 fois, 0,5 fois l’écart-type… Utilisez dans ce cas la cellule « Facteur pour l’écart-type » pour saisir la valeur souhaitée. Si les classes extrêmes sont trop petites pour contenir toute l’étendue des valeurs de la donnée, elles sont élargies au minimum et au maximum.
Avec un même facteur pour l’écart-type, cette discrétisation donne lieu à seulement deux répartitions en fonction du caractère pair ou impair des classes : en effet, pour tout nombre de classe impair (3, 5, 7, etc.) avec un facteur pour l’écart-type de 1, la classe centrale sera toujours centrée sur la moyenne, et de largeur un écart-type. Pour tout nombre de classe pair avec un facteur pour l’écart-type de 1, la moyenne séparera toutes les classes en deux.
Cette discrétisation n’est pas adaptée aux données relatives : par exemple, si vous cartographiez un pourcentage, la moyenne des données n’est pas la moyenne des pourcentages. Elle est particulièrement adaptée aux données qui présenter beaucoup d’observations proches ou autour de la moyenne. Sa particularité est de mettre bien en évidence les valeurs extrêmes d’une série.
Méthode Standard centrée zéro
Cette discrétisation est identique à la méthode standard, mais les classes sont cette fois centrées sur zéro, et non pas sur la moyenne arithmétique. L’écart-type utilisé comme largeur des classes n’est alors pas calculé de manière classique par rapport à la moyenne, mais par rapport à zéro. Cette méthode est adaptée uniquement au traitement de séries statistiques comportant à la fois des valeurs négatives ou positives. Elle est inutilisable dans les autres cas.
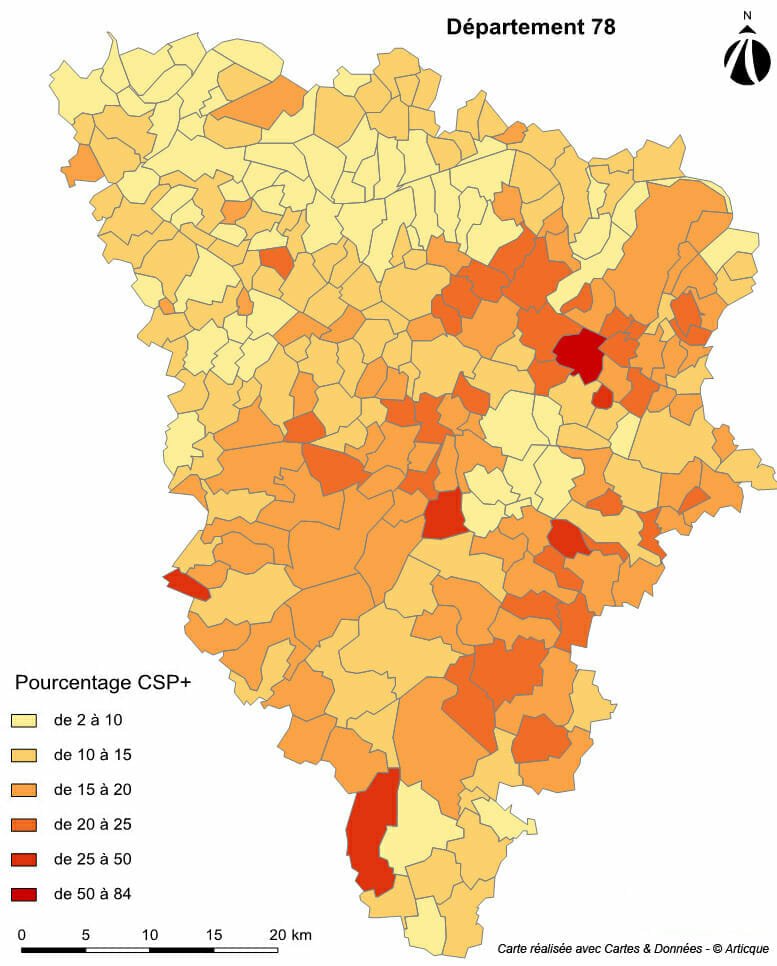
Méthode Quantiles
Les classes sont calculées pour qu’elles contiennent le même nombre d’éléments. La méthode divise donc les observations de la série statistique en X classes composées chacune du même nombre N d’éléments. Elle place ensuite les N plus faibles valeurs dans la 1ere classe, les N suivantes dans la seconde, etc. L’avantage de cette méthode est de mettre en évidence les valeurs faibles et les valeurs fortes. Les classes créées ne se basant que sur le nombre d’éléments qu’elles doivent contenir, cette méthode ne garantit en revanche ni l’homogénéité des classes, ni l’objectivité du découpage.
Méthode Egales étendues
L’étendue de la série (valeur_max – valeur_min) est partagée équitablement entre le nombre de classes à créer.
Ex : pour une donnée allant de 50 à 150 découpée en 5 classes
- Étendue = 150-50 = 100
- Intervalle des classes = 100/5 = 20
- Bornes des classes = [50-70], [70-90], [90-110], [110-130], [130-150]
Cette méthode présente l’intérêt de produire des classes dont les bornes sont plus « régulières » que les autres, donc généralement plus compréhensibles pour les lecteurs. En revanche, elle peut aussi produire des classes vides en cas de dispersions « extrêmes » des données (ex : une grande majorité de valeurs faibles et seulement quelques valeurs extrêmement fortes). Elle est particulièrement utile pour représenter des phénomènes naturels ou environnementaux (distance, temps, températures, altitudes, etc.)
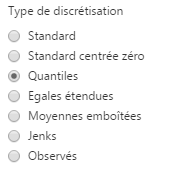
Méthode Moyennes emboîtées
Les classes sont découpées et redécoupées en fonction de la moyenne des données de chaque classe et puis chaque sous-classe.
Cette méthode présente l’avantage de créer des classes assez homogènes et de ne pas être gênée par les dispersions extrêmes : en effet, le calcul des moyennes et sous-moyennes se fait de plus en plus précis et « colle » bien aux données. Elle présente en revanche le désavantage de n’autoriser comme nombre de classes que des puissances de 2 : 2 classes, 4 classes, 8, 16, 32, etc…
Méthode Jenks
La discrétisation de Jenks : Georges Frederick Jenks, cartographe américain du XXe siècle, auteur de méthodes statistiques de classification des données en vue d’optimiser leur représentation sur une carte choroplèthe. Sa méthode repose sur la notion des variances intergroupes et intragroupes. En utilisant cette méthode, le module procède par essais successifs avec pour objectif de minimiser la variance intragroupes (homogénéiser l’intérieur de chaque classe), et à maximiser la variance intergroupes (différencier les classes).
Cette méthode produit généralement les meilleurs résultats en termes de classes à la fois homogènes dans leur composition et distinctes les unes des autres. Cependant, elle peut également se montrer parfois trop « extrême » lorsque la dispersion des valeurs est très irrégulière.
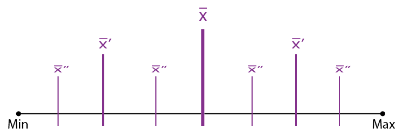
Méthode Observés
La méthode des « seuils observés » permet à l’utilisateur de saisir ses propres bornes de classes. Pour l’utiliser, sélectionnez la méthode Observés, puis cliquez sur « Appliquer » pour valider le choix. Les zones de saisie apparaissent au niveau de la composition des classes.
Les utilisateurs peu habitués à cette opération apprendront très vite à reconnaître la méthode à utiliser pour chaque cas de figure, en s’aidant notamment du graphique de dispersion et de l’indice TAI coloré.
Diagramme de dispersion
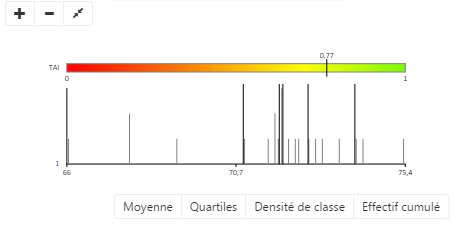
Le graphique de dispersion représente la façon dont les valeurs de la série statistique se répartissent entre le minimum et le maximum. Il permet de visualiser le comportement de la série statistique en un seul regard, et s’avère un support très utile à la discrétisation.
Chaque valeur est représentée par une barre sur le diagramme. Lorsque plusieurs valeurs sont proches ou identiques, les barres qui les représentent s’empilent en hauteur. Les bornes de classes sont représentées à l’aide de lignes pointillées. Lorsque vous utilisez la méthode Observés, des carrés noirs apparaissent sur les bornes de classes pour vous permettre de les déplacer horizontalement.
Il permet d’afficher :
- la courbe des effectifs cumulés (en bleu) qui complète le diagramme en fréquence (en noir).
- un diagramme en densité (en rouge), représentant chaque classe avec une hauteur H calculée comme suit : H = nombre d’éléments dans la classe/largeur de la classe
- les quartiles (en jaune) qui sont indiqués sur l’axe des abscisses du diagramme
- la moyenne qui s’affiche en vert sur l’axe des abscisses
L’indice TAI (Tabular Accuracy Index)
L’indice TAI (Tabular Accuracy Index) est une valeur de synthèse qui estime la qualité de la discrétisation.
Plus l’indice TAI est proche de 1, mieux la discrétisation retranscrit fidèlement la dispersion des données au sein de ses classes. On considère généralement que la discrétisation est « utilisable » (ses classes retranscrivent de manière suffisamment fidèle la dispersion réelle des valeurs) lorsque le TAI devient supérieur ou égal à 0,65 / 0,7.
Optimisation du TAI et nombre de classes :
En utilisant le module Discrétisation, vous pouvez parfois être tentés de produire de nombreuses classes pour que le TAI soit proche de 1. En effet, Plus le nombre de classes augmente, plus le TAI se rapproche de 1. Cependant,un nombre de classe trop important (supérieur à 7) nuit à la lisibilité de la carte et à la transmission de l’information qu’elle contient. Ainsi, dans certains cas, il sera préférable de choisir un nombre de classe restreint ou moindre (ex : 5) lorsque l’augmentation du nombre de classes n’induit plus qu’une faible amélioration du TAI.
Onglet Statistiques
Le module Discrétisation précise également un ensemble d’informations statistiques pour vous aider à mieux comprendre votre série de données et à déterminer de manière optimale sa classification :
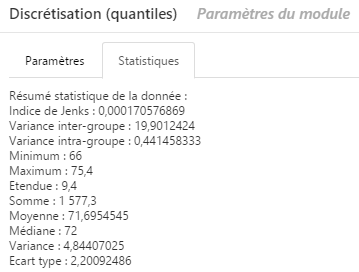
L’onglet Statistiques contient le résumé de la variable étudiée, sous forme de différents indices/valeurs significatifs.
Indice de Jenks
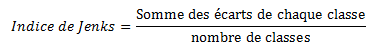
- L’indice de Jenks synthétise l’homogénéité des valeurs à l’intérieur de chaque classe, et l’hétérogénéité des classes entre elles.
- Plus il est proche de zéro, plus les classes sont homogènes dans leur composition et nettement différenciées entre elles (« bonne » discrétisation).
Variance Inter/Intragroupes
La variance est une mesure servant à caractériser la dispersion des effectifs d’une série statistique.
- Intergroupes : caractérise la dispersion des classes
Cet indice indique si les valeurs à l’intérieur des classes obtenues sont homogènes ou disparates. Une variance intragroupe faible indique des valeurs homogènes à l’intérieur de chaque classe.
Autres valeurs significatives :
- la valeur « minimum » en statistique est la plus petite valeur que l’on retrouve dans une population.
- la valeur « maximum » en statistique est la plus grande valeur que l’on retrouve dans une population.
- la moyenne est une mesure (statistique) caractérisant les éléments d’un ensemble de quantités : elle exprime la grandeur qu’aurait chacun des membres de l’ensemble s’ils étaient tous identiques sans changer la dimension globale de l’ensemble.
- l’étendue d’une série statistique est la différence entre la plus grande et la plus petite des valeurs du caractère.
- la médiane permet de découper deux contenant le même nombre d’individu.
- l’écart type mesure la dispersion d’un effectif autour de leur moyenne.
Articque est le pionnier français de la prise de décision stratégique grâce à la cartographie. Editeur de solutions géodécisionnelles depuis plus de 30 ans, nous aidons les organismes et entreprises à mieux piloter leurs activités et à éclairer leurs décisions. Elles gagnent ainsi en performance grâce à une connaissance approfondie de leur territoire.
ARTICQUE - TOURS,
149 avenue du Général de Gaulle,
37230 Fondettes – France
02 47 49 90 49