Présentation du module Régression
La régression linéaire est une méthode qui permet d’estimer à quel point un phénomène en explique un autre. On vérifie s’il y a ou non corrélation entre deux variables.
Le module Régression fournit dans sa fenêtre de paramétrage le graphique en nuage de points, la droite de régression et le coefficient de corrélation linéaire qui permettent d’estimer et de qualifier le rapport entre les deux phénomènes.
Vous pouvez par exemple :
- S’il existe une relation entre les votes pour un parti à une élection et un phénomène socio-économique
- Vérifier le rapport entre votre prospection et vos résultats concrets.
- Estimer s’il existe une relation entre la distance qui vous sépare de vos clients (zone de chalandise) et le chiffre d’affaires généré.
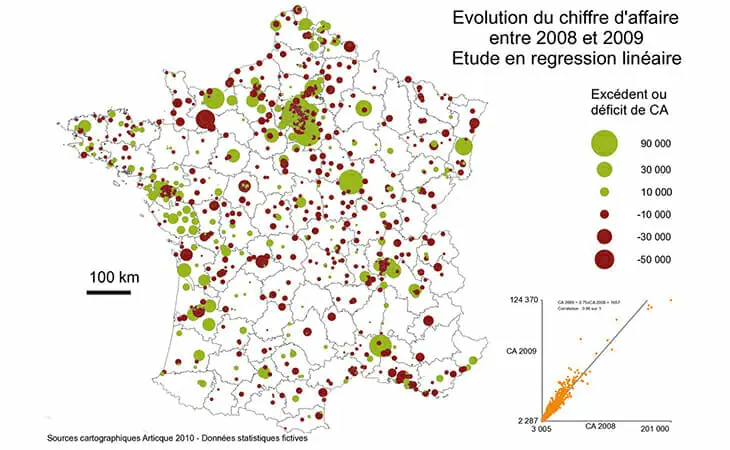
Le module Régression produit également des données qui peuvent être cartographiées, afin de visualiser les résultats de vos études sur les individus ou les territoires.
Fonctionnement du module Régression
Le module Régression permet de comparer des variables entre elles sur un ensemble de territoires afin d’analyser leur relation selon différentes méthodes de régression.
Les méthodes de régression statistique permettent de vérifier s’il existe une relation entre les variables, d’observer de quel type de relation il s’agit et leur degré de corrélation (l’intensité de la relation/liaison qui peut exister entre les variables).
Il est possible d’effectuer différents types de régression à partir des données en entrée :
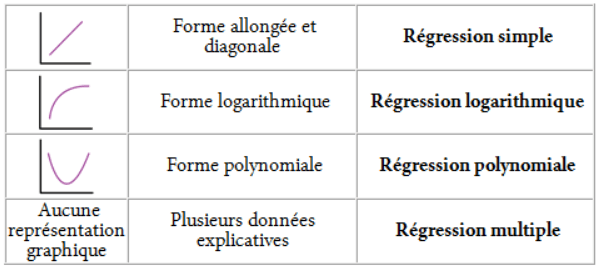
- simple : relation linéaire entre 2 variables, dans laquelle l’augmentation ou la diminution commune est constante. La relation suit une équation de type y=ax+b.
- polynomiale : la relation entre les 2 variables est de type non linéaire et suit un polynôme de type y=a+bx+cx² (exemple : alternance conjointe d’augmentation/diminution/augmentation)
- logarithmique : la relation entre 2 variables est de type logarithmique. Elle montre une augmentation conjointe très forte au début puis un ralentissement (exemple : fréquentation d’un nouveau site web qui serait très forte au début puis s’essoufflerait au fil du temps)
- multiple : utilisation de plusieurs variables explicatives.
En termes de résultats, le module Régression :
- effectue une représentation graphique (nuage de points + courbe/droite de régression) de la relation entre les variables étudiées.
- fournit un ensemble d’indicateurs permettant de comprendre et d’analyser la relation entre les variables.
- génère des résidus de régression, c’est à dire l’estimation pour chaque territoire de la façon dont il s’écarte de la relation « estimée ».
- crée une classification des territoires selon la méthode K-means. L’algorithme K-means de partitionnement de données est une méthode dont le but est de diviser des observations en K partitions (clusters) dans lesquelles chaque observation appartient à la partition avec la moyenne la plus proche, sous la forme d’une donnée qualitative.
Graphique de régression
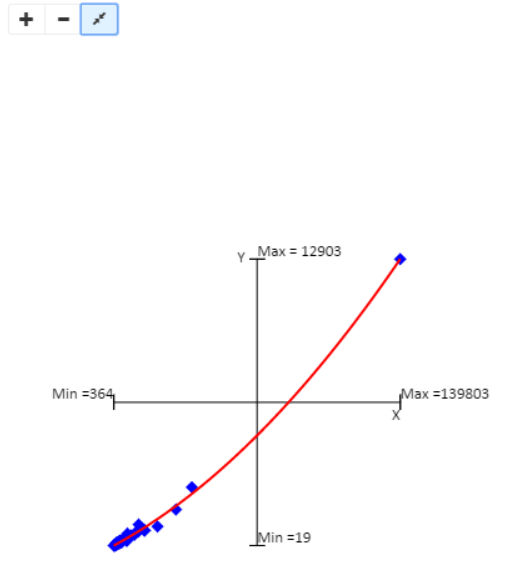
Le module crée une représentation des variables sur un graphique en nuage de points :
- les axes X et Y correspondent aux variables explicatives et à expliquer.
- chaque point bleu représente un territoire étudié, et se positionne sur le graphique selon sa valeur dans les 2 variables
- la ligne rouge représente la droite/courbe de régression
La droite/courbe de régression dessine la tendance générale du nuage en passant au plus proche de l’ensemble des points (on parle également de « droite des moindres carrés »). C’est un modèle de prédiction de ce que devrait être la valeur de chaque territoire du fait de la tendance générale qui se dégage.
Une analyse visuelle de la forme du nuage de points et de sa proximité à la droite/courbe de régression permettent déjà une première estimation de la nature de la relation et de sa force.
Choix du type de régression
Le type de régression choisi dépend du type de relation que l’on souhaite mettre en évidence ou vérifier entre les variables étudiées.
La forme du nuage observée sur le graphique permet d’estimer le type de régression le mieux adapté :
À partir du tableau d’origine, les calculs et transformations suivants sont effectués :
- standardisation des données par un codage disjonctif complet, qui a pour finalité de transformer des variables qualitatives en variables quantitatives.
- constitution du tableau des fréquences
- constitution de la matrice d’inertie selon la métrique de chi²
- calcul des coordonnées (valeurs des projections sur les axes factoriels), de la contribution (part d’un point i ou j à l’inertie expliquée par le facteur) et des qualités de représentation
Classification
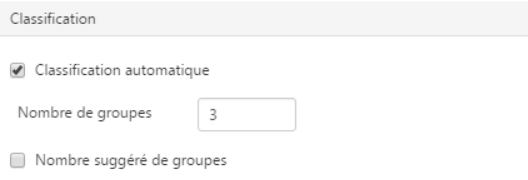
Vous pouvez effectuer une classification de vos territoires, de manière à rassembler en groupes ceux qui ont un profil identique vis à vis des données étudiées. La solution Cartes & Données Online utilise la méthode de classification automatique K-means.
Interprétation des résultats
Coefficient de corrélation
Le coefficient de corrélation permet d’estimer s’il y a ou non corrélation, ainsi que la force de la relation.
Valeur du coefficient de corrélation :
• le coefficient varie entre -1 et 1
• plus sa valeur est proche de 0, moins il y a corrélation entre les variables
• plus sa valeur est proche de 1 ou -1, plus la corrélation est forte.
• on peut raisonnablement commencer à dire qu’une corrélation existe entre X et Y au dessus de 0,65 ou en dessous de -0,65.
Le signe placé devant ce coefficient indique :
• s’il est positif, qu’il y a augmentation simultanée des deux variables
• s’il est négatif, qu’il y a anti-corrélation (l’augmentation de X entraîne la diminution de Y et inversement).
Coefficient de détermination
Le coefficient de détermination varie entre 0 et 1. Il exprime l’ajustement du nuage de points par rapport au modèle prédictif (la droite/courbe de régression).
• Plus sa valeur est proche de 0, moins le modèle est ajusté par rapport au nuage de points
• Plus sa valeur est proche de 1, plus le modèle est ajusté par rapport au nuage de points
Résidu de régression
Le résultat du module est, par défaut, une donnée continue qui correspond aux résidus de régression.
Les résidus de régression expriment l’écart de chaque point du nuage (les données observées) par rapport à la droite/courbe de régression (la tendance) :
• les résidus peuvent avoir une valeur positive ou négative, selon que le point se situe au dessus (+) ou en dessous (-) de la droite/courbe de régression.
• plus la valeur du résidu est élevée (en positif ou en négatif), plus un territoire s’écarte de la tendance générale.
• mieux le type de régression est choisi, plus les résidus seront précis.
Classes
En cas d’utilisation de la fonction de classification, le module produit également une donnée qualitative qui correspond à l’intitulé de chaque classe.
Notre mission : rester l'éditeur de référence au niveau mondial de solutions hors du commun dédiées à l'analyse exploratoire de données localisées, à leur exploitation et à leur communication.
ARTICQUE - TOURS,
149 avenue du Général de Gaulle,
37230 Fondettes – France
02 47 49 90 49
ARTICQUE - PARIS,
23 rue du Départ
75014 Paris – France
01 49 88 84 64
